Lie Group and Lie Algebra (2)

4. Lie Group and Lie Algebra (2)

이전 포스팅에 이어서 계속

4.2 Exponential and Logarithmic Mapping

4.2.1 Exponential Map of $\text{SO}(3)$

$\exp \left(\phi^{\wedge}\right)$ 를 어떻게 구할까? → 지수함수의 테일러 전개 이용

\[\exp \left(\phi^{\wedge}\right)=\sum_{n=0}^{\infty} \cfrac{1}{n !}\left(\phi^{\wedge}\right)^{n}\]

$\phi$ 는 3차원 벡터이므로 방향과 길이가 있다

그러므로

\(\phi=\theta \mathbf{n}\) ($\theta$ 는 길이, $\textbf{n}$ 은 길이가 1인 방향벡터)

그리고 $\textbf{n}$ 은 다음과 같은 두가지 성질이 있다.

\[\begin{array}{c}\mathbf{n}^{\wedge} \mathbf{n}^{\wedge}=\left[\begin{array}{ccc}-n_{2}^{2}-n_{3}^{2} & n_{1} n_{2} & n_{1} n_{3} \\n_{1} n_{2} & -n_{1}^{2}-n_{3}^{2} & n_{2} n_{3} \\n_{1} n_{3} & n_{2} n_{3} & -n_{1}^{2}-n_{2}^{2}\end{array}\right]=\mathbf{n} \mathbf{n}^{\mathrm{T}}-\mathbf{I} \end{array}\] \[\mathbf{n}^{\wedge} \mathbf{n}^{\wedge} \mathbf{n}^{\wedge}=\mathbf{n}^{\wedge}\left(\mathbf{n} \mathbf{n}^{\mathrm{T}}-\mathbf{I}\right)=-\mathbf{n}^{\wedge}\]

이 성질들을 이용하여 $\exp \left(\phi^{\wedge}\right)$ 를 정리하면,

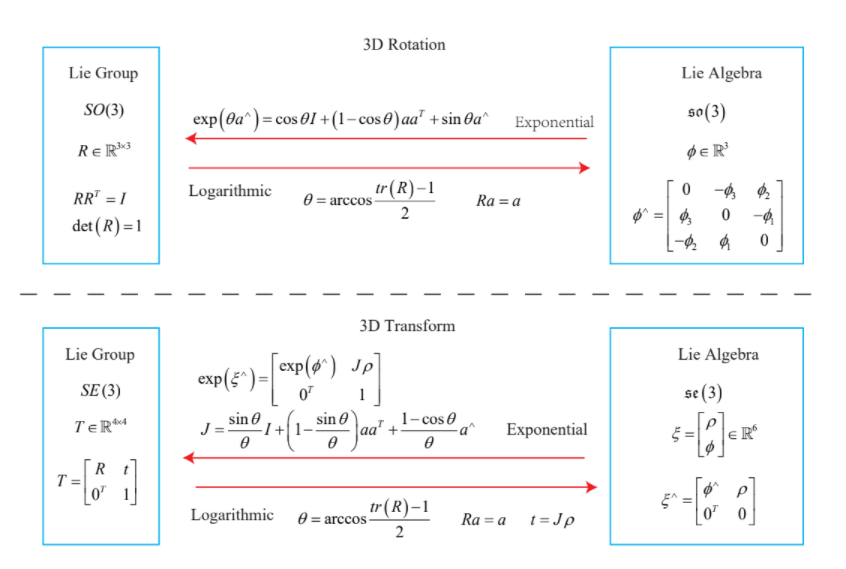
\[\begin{aligned}\exp \left(\phi^{\wedge}\right) &=\exp \left(\theta \mathbf{n}^{\wedge}\right)=\sum_{n=0}^{\infty} \frac{1}{n !}\left(\theta \mathbf{n}^{\wedge}\right)^{n} \\&=\mathbf{I}+\theta \mathbf{n}^{\wedge}+\frac{1}{2 !} \theta^{2} \mathbf{n}^{\wedge} \mathbf{n}^{\wedge}+\frac{1}{3 !} \theta^{3} \mathbf{n}^{\wedge} \mathbf{n}^{\wedge} \mathbf{n}^{\wedge}+\frac{1}{4 !} \theta^{4}\left(\mathbf{n}^{\wedge}\right)^{4}+\ldots \\&=\mathbf{n} \mathbf{n}^{\mathrm{T}}-\mathbf{n}^{\wedge} \mathbf{n}^{\wedge}+\theta \mathbf{n}^{\wedge}+\frac{1}{2 !} \theta^{2} \mathbf{n}^{\wedge} \mathbf{n}^{\wedge}-\frac{1}{3 !} \theta^{3} \mathbf{n}^{\wedge}-\frac{1}{4 !} \theta^{4}\left(\mathbf{n}^{\wedge}\right)^{2}+\ldots \\&=\mathbf{n} \mathbf{n}^{\mathrm{T}}+\underbrace{\left(\theta-\frac{1}{3 !} \theta^{3}+\frac{1}{5 !} \theta^{5}-\ldots\right)}_{\sin \theta} \mathbf{n}^{\wedge}-\underbrace{\left(1-\frac{1}{2 !} \theta^{2}+\frac{1}{4 !} \theta^{4}-\ldots\right)}_{\cos \theta} \mathbf{n}^{\wedge} \mathbf{n}^{\wedge} \\&=\mathbf{n}^{\wedge} \mathbf{n}^{\wedge}+\mathbf{I}+\sin \theta \mathbf{n}^{\wedge}-\cos \theta \mathbf{n}^{\wedge} \mathbf{n}^{\wedge} \\&=(1-\cos \theta) \mathbf{n}^{\wedge} \mathbf{n}^{\wedge}+\mathbf{I}+\sin \theta \mathbf{n}^{\wedge} \\&=\cos \theta \mathbf{I}+(1-\cos \theta) \mathbf{n} \mathbf{n}^{\mathrm{T}}+\sin \theta \mathbf{n}^{\wedge} .\end{aligned}\] \[\exp \left(\theta \mathbf{n}^{\wedge}\right)=\cos \theta \mathbf{I}+(1-\cos \theta) \mathbf{n} \mathbf{n}^{\mathrm{T}}+\sin \theta \mathbf{n}^{\wedge}\]

정리된 결과는 로드리게스식과 같다

이 결과에서 알 수 있는 것은 \(\mathfrak{so}(3)\) 은 rotation vector이며, 모든 \(\mathfrak{so}(3)\) 에 속하는 vector는 \(\text{SO}(3)\) 로 대응 될 수 있다는 점이다

이에 역으로 Logarithmic map을 생각할 수 있는데 다음과 같다

\[\phi=\ln (\mathbf{R})^{\vee}=\left(\sum_{n=0}^{\infty} \cfrac{(-1)^{n}}{n+1}(\mathbf{R}-\mathbf{I})^{n+1}\right)^{\vee}\]

$\text{SO}(3)$ 에 대응되는 $\mathfrak{so}(3)$ 는 유일함. 하지만 $\mathfrak{so}(3)$ 에 대응되는 $\text{SO}(3)$ 는 여러개. 즉, 일대일 대응이 아님 (360도를 생각해보자) 그래서 각도를 $-\pi,\pi$ 로 제한시킨다 (범위를 제한하면 일대일 대응이 됨)

4.2.2 Exponential Map of $\text{SO}(3)$

\[\begin{aligned}\exp \left(\boldsymbol{\xi}^{\wedge}\right) &=\left[\begin{array}{cc}\sum_{n=0}^{\infty} \frac{1}{n !}\left(\boldsymbol{\phi}^{\wedge}\right)^{n} & \sum_{n=0}^{\infty} \frac{1}{(n+1) !}\left(\boldsymbol{\phi}^{\wedge}\right)^{n} \boldsymbol{\rho} \\\mathbf{0}^{\mathrm{T}} & 1\end{array}\right] \\& \triangleq\left[\begin{array}{cc}\mathbf{R} & \mathbf{J} \rho \\\mathbf{0}^{\mathrm{T}} & 1\end{array}\right]=\mathbf{T} .\end{aligned}\]

길게 설명안함

\[\begin{aligned}\sum_{n=0}^{\infty} \frac{1}{(n+1) !}\left(\boldsymbol{\phi}^{\wedge}\right)^{n} &=\mathbf{I}+\frac{1}{2 !} \theta \mathbf{a}^{\wedge}+\frac{1}{3 !} \theta^{2}\left(\mathbf{a}^{\wedge}\right)^{2}+\frac{1}{4 !} \theta^{3}\left(\mathbf{a}^{\wedge}\right)^{3}+\frac{1}{5 !} \theta^{4}\left(\mathbf{a}^{\wedge}\right)^{4} \ldots \\&=\frac{1}{\theta}\left(\frac{1}{2 !} \theta^{2}-\frac{1}{4 !} \theta^{4}+\cdots\right)\left(\mathbf{a}^{\wedge}\right)+\frac{1}{\theta}\left(\frac{1}{3 !} \theta^{3}-\frac{1}{5} \theta^{5}+\cdots\right)\left(\mathbf{a}^{\wedge}\right)^{2}+\mathbf{I} \\&=\frac{1}{\theta}(1-\cos \theta)\left(\mathbf{a}^{\wedge}\right)+\frac{\theta-\sin \theta}{\theta}\left(\mathbf{a a}^{T}-\mathbf{I}\right)+\mathbf{I} \\&=\frac{\sin \theta}{\theta} \mathbf{I}+\left(1-\frac{\sin \theta}{\theta}\right) \mathbf{a a}^{T}+\frac{1-\cos \theta}{\theta} \mathbf{a}^{\wedge} \triangleq \mathbf{J} .\end{aligned}\] \[\mathbf{J}=\cfrac{\sin \theta}{\theta} \mathbf{I}+\left(1-\cfrac{\sin \theta}{\theta}\right) \mathbf{a a}^{\mathrm{T}}+\cfrac{1-\cos \theta}{\theta} \mathbf{a}^{\wedge}\]

요약하면 다음과 같음

4.3 Lie Algebra Derivation and Perturbation Model

4.3.1 BCH Formula and its Approximation

다음은 아쉽게도 참이 아니다

\(\ln (\exp (\mathbf{A}) \exp (\mathbf{B}))=\mathbf{A}+\mathbf{B}\) (A,B는 행렬)

BHC 공식을 이용

\[\ln (\exp (\mathbf{A}) \exp (\mathbf{B}))=\mathbf{A}+\mathbf{B}+\frac{1}{2}[\mathbf{A}, \mathbf{B}]+\frac{1}{12}[\mathbf{A},[\mathbf{A}, \mathbf{B}]]-\frac{1}{12}[\mathbf{B},[\mathbf{A}, \mathbf{B}]]+\cdots\]

[ , ]는 앞서 말한 Lie bracket임

$\phi_{1}$ 와 $\phi_{2}$ 가 작을 경우 다음이 성립

\[\ln \left(\exp \left(\boldsymbol{\phi}_{1}^{\wedge}\right) \exp \left(\boldsymbol{\phi}_{2}^{\wedge}\right)\right)^{\vee} \approx\left\{\begin{array}{ll}\mathbf{J}_{l}\left(\boldsymbol{\phi}_{2}\right)^{-1} \boldsymbol{\phi}_{1}+\boldsymbol{\phi}_{2} & \text { when } \boldsymbol{\phi}_{1} \text { is a small amount } \\\mathbf{J}_{r}\left(\boldsymbol{\phi}_{1}\right)^{-1} \boldsymbol{\phi}_{2}+\boldsymbol{\phi}_{1} & \text { when } \boldsymbol{\phi}_{2} \text { is a small amount. }\end{array}\right.\] \[\mathbf{J}_{l}=\mathbf{J}=\frac{\sin \theta}{\theta} \mathbf{I}+\left(1-\frac{\sin \theta}{\theta}\right) \mathbf{a a}^{\mathrm{T}}+\frac{1-\cos \theta}{\theta} \mathbf{a}^{\wedge}\] \[\mathbf{J}_{l}^{-1}=\frac{\theta}{2} \cot \frac{\theta}{2} \mathbf{I}+\left(1-\frac{\theta}{2} \cot \frac{\theta}{2}\right) \mathbf{a a}^{\mathrm{T}}-\frac{\theta}{2} \mathbf{a}^{\wedge}\] \[\mathbf{J}_{r}(\boldsymbol{\phi})=\mathbf{J}_{l}(-\boldsymbol{\phi})\]

정리하자면

회전행렬 $\textbf{R}$ 이 있고 거기서 $\Delta\textbf{R}$ 만큼 변한다면 $\Delta \mathbf{R} \cdot \mathbf{R}$ 일 것이다.

이를 Lie Algebra로 생각하면

\[\exp \left(\Delta \phi^{\wedge}\right) \exp \left(\phi^{\wedge}\right)=\exp \left(\left(\phi+\mathbf{J}_{l}^{-1}(\phi) \Delta \phi\right)^{\wedge}\right)\]

반대로

Lie Algebra에서 $\phi$ 와 $\Delta\phi$ 가 주어졌을 때

\[\exp \left((\phi+\Delta \phi)^{\wedge}\right)=\exp \left(\left(\mathbf{J}_{l} \Delta \phi\right)^{\wedge}\right) \exp \left(\phi^{\wedge}\right)=\exp \left(\phi^{\wedge}\right) \exp \left(\left(\mathbf{J}_{r} \Delta \phi\right)^{\wedge}\right)\]

$\text{SE}(3)$ 에서 BHC 공식을 적용시키면 다음과 같다.

\[\begin{array}{l}\exp \left(\Delta \boldsymbol{\xi}^{\wedge}\right) \exp \left(\boldsymbol{\xi}^{\wedge}\right) \approx \exp \left(\left(\mathcal{J}_{l}^{-1} \Delta \boldsymbol{\xi}+\boldsymbol{\xi}\right)^{\wedge}\right) \\\exp \left(\boldsymbol{\xi}^{\wedge}\right) \exp \left(\Delta \boldsymbol{\xi}^{\wedge}\right) \approx \exp \left(\left(\mathcal{J}_{r}^{-1} \Delta \boldsymbol{\xi}+\boldsymbol{\xi}\right)^{\wedge}\right)\end{array}\]

4.3.2 Derivative on $\text{SO}(3)$

SLAM에서 pose를 optimization한다는 것은 error function을 정의한 후 이 error를 최소화 시키는 것이다.

로봇이 돌아다니면서 관찰된 point를 통해 observation data $\textbf{z}$ 를 생성한다.

\[\mathbf{z}=\mathbf{T p}+\mathbf{w}\]

($\textbf{w}$ 는 noise)

이 noise 때문에 실제값과 관찰값에 대한 차이(error)가 생기게 된다

\[\mathbf{e}=\mathbf{z}-\mathbf{T p}\]

이를 이용해 앞에서 말한 error function을 정의하면 다음과 같다

\[\min_{\mathbf{T}} J(\mathbf{T})=\sum_{i=1}^{N}\left\|\mathbf{z}_{i}-\mathbf{T} \mathbf{p}_{i}\right\|_{2}^{2}\]

이를 $\textbf{T}$ 에 대해 미분하여 $J$ 의 최소값을 찾는 이것이 error가 가장 작은 pose를 찾는 것이다.(optimization)

4.3.3 Derivative Model

우선 point $\textbf{p}$ 에 $\textbf{R}$ rotation을 적용한 $\textbf{Rp}$ 를 $\textbf{R}$ 로 미분하는 상황을 생각해보자

\[\cfrac{\partial(\mathbf{R} \mathbf{p})}{\partial \mathbf{R}}\]

어떻게 미분할지 모르겠다

여기서 $\textbf{R}$ 에서 $\phi$ 로 대응되는 lie algebra를 이용한다

\[\begin{aligned}\frac{\partial\left(\exp \left(\boldsymbol{\phi}^{\wedge}\right) \mathbf{p}\right)}{\partial \boldsymbol{\phi}} &=\lim _{\delta \boldsymbol{\phi} \rightarrow \mathbf{0}} \frac{\exp \left((\boldsymbol{\phi}+\delta \boldsymbol{\phi})^{\wedge}\right) \mathbf{p}-\exp \left(\boldsymbol{\phi}^{\wedge}\right) \mathbf{p}}{\delta \boldsymbol{\phi}} \\&=\lim _{\delta \boldsymbol{\phi} \rightarrow \mathbf{0}} \frac{\exp \left(\left(\mathbf{J}_{l} \delta \boldsymbol{\phi}\right)^{\wedge}\right) \exp \left(\boldsymbol{\phi}^{\wedge}\right) \mathbf{p}-\exp \left(\boldsymbol{\phi}^{\wedge}\right) \mathbf{p}}{\delta \boldsymbol{\phi}} \\&=\lim _{\delta \boldsymbol{\phi} \rightarrow \mathbf{0}} \frac{\left(\mathbf{I}+\left(\mathbf{J}_{l} \delta \boldsymbol{\phi}\right)^{\wedge}\right) \exp \left(\boldsymbol{\phi}^{\wedge}\right) \mathbf{p}-\exp \left(\boldsymbol{\phi}^{\wedge}\right) \mathbf{p}}{\delta \boldsymbol{\phi}} \\&=\lim _{\delta \boldsymbol{\phi} \rightarrow \mathbf{0}} \frac{\left(\mathbf{J}_{l} \delta \boldsymbol{\phi}\right)^{\wedge} \exp \left(\boldsymbol{\phi}^{\wedge}\right) \mathbf{p}}{\delta \boldsymbol{\phi}} \\&=\lim _{\delta \boldsymbol{\phi} \rightarrow \mathbf{0}} \frac{-\left(\exp \left(\boldsymbol{\phi}^{\wedge}\right) \mathbf{p}\right)^{\wedge} \mathbf{J}_{l} \delta \boldsymbol{\phi}}{\delta \boldsymbol{\phi}}=-(\mathbf{R} \mathbf{p})^{\wedge} \mathbf{J}_{l}\end{aligned}\]

하지만 결과로 나온 $\textbf{J}_l$ 도 구하기가 쉽지 않으므로 “Perturbation Model”을 이용한다.

4.3.4 Perturbation Model

$\textbf{R}$ 의 변화량 $\Delta\textbf{R}$ 을 생각해보자.

$\Delta\textbf{R}$ 은 행렬 $\textbf{R}$ 에 오른쪽이나 왼쪽에 곱해져서 $\textbf{R}$ 에서 $\Delta\textbf{R}$ 만큼 변한 행렬을 찾을 수 있다.

$\Delta\textbf{R}$ 에 대응되는 Lie algebra를 $\varphi$ 라고 한다면

\[\begin{aligned}\frac{\partial(\mathbf{R p})}{\partial \varphi} &=\lim _{\varphi \rightarrow 0} \frac{\exp \left(\varphi^{\wedge}\right) \exp \left(\phi^{\wedge}\right) \mathbf{p}-\exp \left(\phi^{\wedge}\right) \mathbf{p}}{\varphi} \\&=\lim _{\varphi \rightarrow 0} \frac{\left(\mathbf{I}+\varphi^{\wedge}\right) \exp \left(\phi^{\wedge}\right) \mathbf{p}-\exp \left(\phi^{\wedge}\right) \mathbf{p}}{\varphi} \\&=\lim _{\varphi \rightarrow 0} \frac{\varphi^{\wedge} \mathbf{R p}}{\varphi}=\lim _{\varphi \rightarrow 0} \frac{-(\mathbf{R p})^{\wedge} \varphi}{\varphi}=-(\mathbf{R p})^{\wedge}\end{aligned}\]

결과를 봤을 때 아까와는 다르게 $\textbf{J}_l$ 을 구할 필요가 없다.

4.3.5 Derivative on $\text{SE}(3)$

$\text{SE}(3)$ 의 경우도 마찬가지로 생각하여 유도하면

\[\begin{aligned}\frac{\partial(\mathbf{T p})}{\partial \delta \boldsymbol{\xi}} &=\lim _{\delta \boldsymbol{\xi} \rightarrow 0} \frac{\exp \left(\delta \boldsymbol{\xi}^{\wedge}\right) \exp \left(\boldsymbol{\xi}^{\wedge}\right) \mathbf{p}-\exp \left(\boldsymbol{\xi}^{\wedge}\right) \mathbf{p}}{\delta \boldsymbol{\xi}} \\&=\lim _{\delta \boldsymbol{\xi} \rightarrow 0} \frac{\left(\mathbf{I}+\delta \boldsymbol{\xi}^{\wedge}\right) \exp \left(\boldsymbol{\xi}^{\wedge}\right) \mathbf{p}-\exp \left(\boldsymbol{\xi}^{\wedge}\right) \mathbf{p}}{\delta \boldsymbol{\xi}} \\&=\lim _{\delta \boldsymbol{\xi} \rightarrow 0} \frac{\delta \boldsymbol{\xi}^{\wedge} \exp \left(\boldsymbol{\xi}^{\wedge}\right) \mathbf{p}}{\delta \boldsymbol{\xi}} \\&=\lim _{\delta \boldsymbol{\xi} \rightarrow 0} \frac{\left[\begin{array}{cc}\delta \boldsymbol{\phi}^{\wedge} & \delta \boldsymbol{\rho} \\\mathbf{0}^{\mathrm{T}} & 0\end{array}\right]\left[\begin{array}{c}\mathbf{R} \mathbf{p}+\mathbf{t} \\1\end{array}\right]}{\delta \boldsymbol{\xi}} \\&=\lim _{\delta \boldsymbol{\xi} \rightarrow 0} \frac{\left[\begin{array}{c}\delta \boldsymbol{\phi}^{\wedge}(\mathbf{R p}+\mathbf{t})+\delta \boldsymbol{\rho} \\\mathbf{0}^{\mathrm{T}}\end{array}\right]}{[\delta \boldsymbol{\rho}, \delta \boldsymbol{\phi}]^{\mathrm{T}}}=\left[\begin{array}{cc}\mathbf{I} & -(\mathbf{R p}+\mathbf{t})^{\wedge} \\\mathbf{0}^{\mathrm{T}} & \mathbf{0}^{\mathrm{T}}\end{array}\right] \triangleq(\mathbf{T p})^{\odot}\end{aligned}\]