Lie Group and Lie Algebra (1)

4. Lie Group and Lie Algebra (1)

이 책을 통틀어 제일 힘들었던 파트다. (사실 지금도 이해했는지 잘 모르겠다)

책을 봐도 뭐라고 하는지 모르겠고 구글에 검색해도 수학과스러운 말들뿐…

Lie Group과 Lie Algebra에 대해 수학과처럼 정확하게는 모르지만 내 나름대로 이해한 내용을 정리 해보려한다.

---

4.1 Basics of Lie Group and Lie Algebra

우선 이걸 왜 배울까?

결론부터 말하자면 SLAM에서 Pose를 최적화(Optimization) 할 때 제약조건을 피하기 위해서다.

도데체 어떤 제약조건이 있길래?

먼저 회전행렬에 대해서 살펴보자

2차원 회전행렬은 단위 원에서만 움직이는 제약조건이 있다.

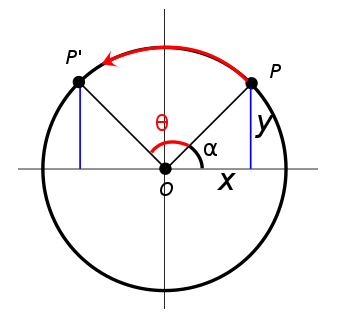
출처: https://ko.wikipedia.org/wiki/회전변환행렬

이는 3차원,4차원 등등 n차원에서도 마찬가지이며 식으로 표현하면

\[\mathbf{R} \mathbf{R}^{\mathrm{T}}=\mathbf{I}, \operatorname{det}(\mathbf{R})=1\]

이 된다.

우리는 이러한 3차원 회전행렬의 집합을 다음과 같이 표현할 수 있다.

\[\mathrm{SO}(3)=\left\{\mathbf{R} \in \mathbb{R}^{3 \times 3} \mid \mathbf{R} \mathbf{R}^{\mathrm{T}}=\mathbf{I}, \operatorname{det}(\mathbf{R})=1\right\}\]

$\text{SO}$ 는 Special Orthogonal Group라는 의미인데 이 집합의 가장 큰 문제가 있다.

바로 “덧셈에 대해 닫혀있지 않다”는 것!

예를 들어 360도를 두 번 회전한다면?

\(\left[\begin{matrix}1 & 0 \\ 0 & 1\end{matrix}\right] + \left[\begin{matrix}1 & 0 \\ 0 & 1\end{matrix}\right] = \left[\begin{matrix}2 & 0 \\ 0 & 2\end{matrix}\right]\) ??

회전행렬에서는 단순히 두 행렬을 더한다고 회전행렬이 되지 않는다.

그러면 어느 연산에 닫혀있을까?

답은 다들 알다시피 곱셈에 대해 닫혀있다

360도를 두번 회전한다면?

\(\left[\begin{matrix}1 & 0 \\ 0 & 1\end{matrix}\right] \left[\begin{matrix}1 & 0 \\ 0 & 1\end{matrix}\right] = \left[\begin{matrix}1 & 0 \\ 0 & 1\end{matrix}\right]\) 제자리!

다시 돌아가서 제약조건은 optimization을 어렵게 만드는데 이를 해결하기 위해 Lie Group과 Lie Algebra의 관계를 이용하는 것이다.

출처: https://www.quora.com/What-are-the-advantages-of-using-Lie-Algebra-and-Lie-Group-in-robotics-and-computer-vision

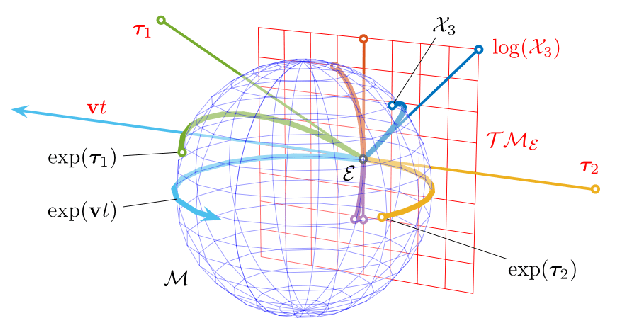
그림에 보이는 구는 3차원 회전행렬의 제약조건이며 뒤에 보이는 평면은 구에 접하는 접평면이다.

Lie theory를 이용해 pose를 optimization 시킨다는 것은 회전행렬을 접평면에 projection시켜 제약조건이 없는 평면에서 optimization을 수행하고, optimization이 끝난 결과를 구에 projection을 시킨다는 의미다.

이렇게 하면 회전행렬의 제약조건을 피하고 pose를 최적화 할 수 있게된다.

재미있게도 Lie Group과 Lie Algebra의 관계는 서로 exponential과 logarithms의 관계에 있다.

이제 이 둘의 관계를 유도해보자

4.1.1 Group

Group의 대수학적인 정의는 다음과 같다.

어떠한 집합 $G$ 가 연산 $\cdot$ 에 대해 다음이 성립하면 Group이라한다.

$G=(A, \cdot)$

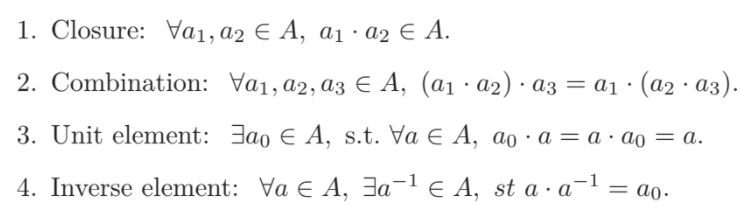
앞서 살펴본 $\text{SO}(3)$ 역시 Group이며 위의 성질을 만족한다.

또한, 회전(Rotation)과 이동(Translation)이 합쳐진 transformation matrix에 대해서도 Group이 존재한다.

\[\operatorname{SE}(3)=\left\{\mathbf{T}=\left[\begin{array}{cc}\mathbf{R} & \mathbf{t} \\\mathbf{0}^{\mathrm{T}} & 1\end{array}\right] \in \mathbb{R}^{4 \times 4} \mid \mathbf{R} \in \mathrm{SO}(3), \mathbf{t} \in \mathbb{R}^{3}\right\}\]

$\text{SE}$ 는 Special Euclidean Group이라는 의미이며 이 집합도 역시 덧셈에 대해 닫혀있지 않다는 제약조건을 안고있다.

Lie Group이란 continuous properties를 가진 Group을 말하며 $\text{SO}(3)$ 와 $\text{SE}(3)$ 는 Rigid Body Motion을 생각할 수 있으므로 Lie Group이다.

4.1.2 Introduction of the Lie Algebra

우선 회전행렬에 대해 Lie Algebra를 유도해보자

\[\mathbf{R} \mathbf{R}^{\mathrm{T}}=\mathbf{I}\] \[\mathbf{R}(t) \mathbf{R}(t)^{T}=\mathbf{I}\] \[\dot{\mathbf{R}}(t) \mathbf{R}(t)^{\mathrm{T}}+\mathbf{R}(t) \dot{\mathbf{R}}(t)^{\mathrm{T}}=0\] \[\dot{\mathbf{R}}(t) \mathbf{R}(t)^{\mathrm{T}}=-\left(\dot{\mathbf{R}}(t) \mathbf{R}(t)^{\mathrm{T}}\right)^{\mathrm{T}}\]

\(\dot{\mathbf{R}}(t) \mathbf{R}(t)^{\mathrm{T}}\) 은 Skew-Symmetric Matrix이므로

\[\dot{\mathbf{R}}(t) \mathbf{R}(t)^{\mathrm{T}}=\phi(t)^{\wedge}\] \[\dot{\mathbf{R}}(t)=\phi(t)^{\wedge} \mathbf{R}(t)=\left[\begin{array}{ccc}0 & -\phi_{3} & \phi_{2} \\\phi_{3} & 0 & -\phi_{1} \\-\phi_{2} & \phi_{1} & 0\end{array}\right] \mathbf{R}(t)\]

$\mathbf{R}(t)$ 를 $t_0=0$ 근방에서 1차 테일러 전개를 하면

\[\begin{aligned}\mathbf{R}(t) & \approx \mathbf{R}\left(t_{0}\right)+\dot{\mathbf{R}}\left(t_{0}\right)\left(t-t_{0}\right) \\&=\mathbf{I}+\boldsymbol{\phi}\left(t_{0}\right)^{\wedge}(t)\end{aligned}\] \[\mathbf{R}(0)=\mathbf{I}\]

여기서 $\phi$ 는 $R$ 의 도함수이므로 SO(3)의 원점에서의 “Tangent Space”라고 부른다.

또한, $t$ 가 $t_0$ 에 가까워질 때 $\phi$ 는 상수가 된다. \(\phi\left(t_{0}\right)=\phi_{0}\)

\[\dot{\mathbf{R}}(t)=\phi\left(t_{0}\right)^{\wedge} \mathbf{R}(t) \approx \phi_{0}^{\wedge} \mathbf{R}(t)\]

이는 미분방정식 꼴이 되므로 최종적으로

\[\mathbf{R}(t)=\exp \left(\boldsymbol{\phi}_{0}^{\wedge} t\right)\]

이 된다

여기에 두 가지 문제가 존재한다

1. $\textbf{R}$ 이 주어졌을 때 $\phi$ 를 찾을 수 있는가?

2. $\phi$ 가 주어졌을 때 $\text{exp}(\phi^\wedge)$ 를 어떻게 구할 것인가 (행렬의 exponential)

4.1.3 The Definition of Lie Algebra

Lie algebra는 origin point(혹은 tangent space)에서 lie group의 local structure를 묘사한다.

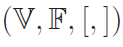
V는 set, F는 scalar field, ,는 binary operation

다음을 만족하면 Lie Algebra라고 한다.

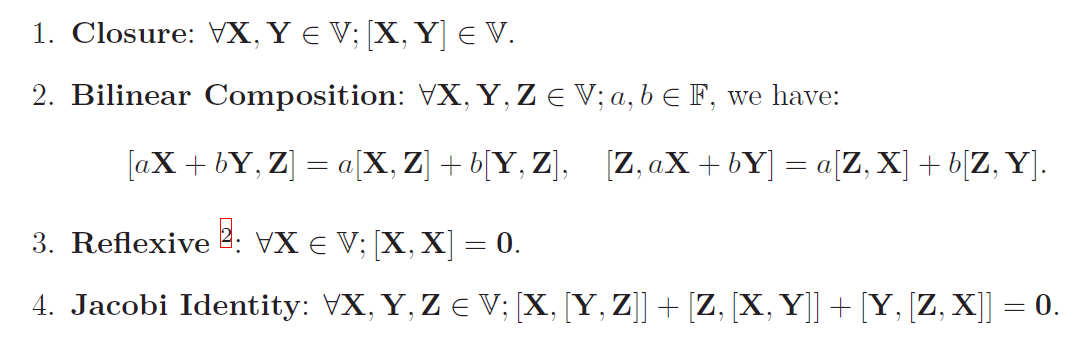
여기서 [ , ]를 Lie bracket이라 함 (Lie Bracket 설명: https://elementary-physics.tistory.com/51)

4.1.4 Lie Algebra $\mathfrak{s o}(3)$

두 벡터 $\phi_1,\ \phi_2$ 의 Lie bracekt은

\[\left[\phi_{1}, \phi_{2}\right]=\left(\Phi_{1} \Phi_{2}-\Phi_{2} \Phi_{1}\right)^{\vee}\]

(이렇게 정의하면 위에서 본 성질에 부합한다)

따라서 다음과 같이 정의가 가능하다.

\[\mathfrak{s o}(3)=\left\{\phi \in \mathbb{R}^{3} \text { or } \boldsymbol{\Phi}=\phi^{\wedge} \in \mathbb{R}^{3 \times 3}\right\}\]

4.1.5 Lie Algebra $\mathfrak{se}(3)$

\[\mathfrak{s e}(3)=\left\{\boldsymbol{\xi}=\left[\begin{array}{l}\boldsymbol{\rho} \\\boldsymbol{\phi}\end{array}\right] \in \mathbb{R}^{6}, \boldsymbol{\rho} \in \mathbb{R}^{3}, \boldsymbol{\phi} \in \mathfrak{s o}(3), \boldsymbol{\xi}^{\wedge}=\left[\begin{array}{ll}\boldsymbol{\phi}^{\wedge} & \boldsymbol{\rho} \\\boldsymbol{0}^{\mathrm{T}} & 0\end{array}\right] \in \mathbb{R}^{4 \times 4}\right\}\]

(유도 안함)

\[\boldsymbol{\xi}^{\wedge}=\left[\begin{array}{ll}\phi^{\wedge} & \rho \\\mathbf{0}^{\mathrm{T}} & 0\end{array}\right] \in \mathbb{R}^{4 \times 4}\]

Lie bracket은

\[\left[\boldsymbol{\xi}_{1}, \boldsymbol{\xi}_{2}\right]=\left(\boldsymbol{\xi}_{1}^{\wedge} \boldsymbol{\xi}_{2}^{\wedge}-\boldsymbol{\xi}_{2}^{\wedge} \boldsymbol{\xi}_{1}^{\wedge}\right)^{\vee}\]

다음에 계속