3D Rigid Body Motion (1)

3. 3D Rigid Body Motion

3.1 Rotation Matrix

3.1.1 Point, Vector and Coordinate System

3D vector

\[\mathbf{a}=\left[\mathbf{e}_{1}, \mathbf{e}_{2}, \mathbf{e}_{3}\right]\left[\begin{array}{l}a_{1} \\ a_{2} \\ a_{3}\end{array}\right]=a_{1} \mathbf{e}_{1}+a_{2} \mathbf{e}_{2}+a_{3} \mathbf{e}_{3}\]

\(\mathbf{e}_{1}, \mathbf{e}_{2}, \mathbf{e}_{3}\) 는 basis

내적

\[\mathbf{a} \cdot \mathbf{b}=\mathbf{a}^{\mathrm{T}} \mathbf{b}=\sum_{i=1}^{3} a_{i} b_{i}=|\mathbf{a}||\mathbf{b}| \cos \langle\mathbf{a}, \mathbf{b}\rangle\]

외적

\[\mathbf{a} \times \mathbf{b}=\left\|\begin{array}{ccc}\mathbf{e}_{1} & \mathbf{e}_{2} & \mathbf{e}_{3} \\a_{1} & a_{2} & a_{3} \\b_{1} & b_{2} & b_{3}\end{array}\right\|=\left[\begin{array}{c}a_{2} b_{3}-a_{3} b_{2} \\ a_{3} b_{1}-a_{1} b_{3} \\ a_{1} b_{2}-a_{2} b_{1}\end{array}\right]=\left[\begin{array}{ccc}0 & -a_{3} & a_{2} \\ a_{3} & 0 & -a_{1} \\ -a_{2} & a_{1} & 0\end{array}\right] \mathbf{b} \triangleq \mathbf{a}^{\wedge} \mathbf{b}\]

여기서 $\mathbf{a}^{\wedge}$ 를 skew-symmetric matrix라고 한다.

\[\mathbf{a}^{\wedge}=\left[\begin{array}{ccc}0 & -a_{3} & a_{2} \\ a_{3} & 0 & -a_{1} \\ -a_{2} & a_{1} & 0\end{array}\right]\]

3.1.2 Euclidean Transforms

Rotation Matrix

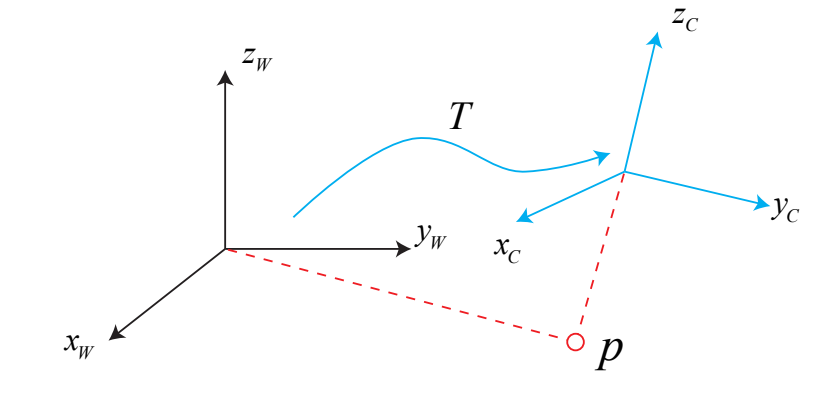
같은 p 벡터지만 coordinate가 다르다.

\[\left[\mathbf{e}_{1}, \mathbf{e}_{2}, \mathbf{e}_{3}\right]\left[\begin{array}{l}a_{1} \\a_{2} \\a_{3}\end{array}\right]=\left[\mathbf{e}_{1}^{\prime}, \mathbf{e}_{2}^{\prime}, \mathbf{e}_{3}^{\prime}\right]\left[\begin{array}{l}a_{1}^{\prime} \\a_{2}^{\prime} \\a_{3}^{\prime}\end{array}\right]\] \[\left[\begin{array}{l}a_{1} \\a_{2} \\a_{3}\end{array}\right]=\left[\begin{array}{lll}\mathbf{e}_{1}^{\mathrm{T}} \mathbf{e}_{1}^{\prime} & \mathbf{e}_{1}^{\mathrm{T}} \mathbf{e}_{2}^{\prime} & \mathbf{e}_{1}^{\mathrm{T}} \mathbf{e}_{3}^{\prime} \\\mathbf{e}_{2}^{\mathrm{T}} \mathbf{e}_{1}^{\prime} & \mathbf{e}_{2}^{\mathrm{T}} \mathbf{e}_{2}^{\prime} & \mathbf{e}_{2}^{\mathrm{T}} \mathbf{e}_{3}^{\prime} \\\mathbf{e}_{3}^{\mathrm{T}} \mathbf{e}_{1}^{\prime} & \mathbf{e}_{3}^{\mathrm{T}} \mathbf{e}_{2}^{\prime} & \mathbf{e}_{3}^{\mathrm{T}} \mathbf{e}_{3}^{\prime}\end{array}\right]\left[\begin{array}{l}a_{1}^{\prime} \\a_{2}^{\prime} \\a_{3}^{\prime}\end{array}\right] \triangleq \mathbf{R} \mathbf{a}^{\prime}\]

$\textbf{R}$ 을 Rotation Matrix로 정의

또한, 회전행렬들만을 모은 집합을 정의할 수 있다.

\[\mathrm{SO}(n)=\left\{\mathbf{R} \in \mathbb{R}^{n \times n} \mid \mathbf{R} \mathbf{R}^{\mathrm{T}}=\mathbf{I}, \operatorname{det}(\mathbf{R})=1\right\}\]

$\text{SO}(n)$ 의 의미는 Special Orthogoanl Group이라는 뜻이며, 이 집합 내에 속한 행렬들은 전부 Rotation Matrix이다. (Group에 대한 자세한 내용은 4장에서 알아보자)

특히 여기서는 n이 3인, $\text{SO}(3)$ 에 대해 다룬다.

앞서 살펴본 벡터는 회전했을 뿐 아니라, 이동한 경우도 생각할 수 있다.

그런경우 다음과 같이 표현한다.

\[\mathbf{a}^{\prime}=\mathbf{R a}+\mathbf{t}\]

$\textbf{a}$ 벡터가 회전( $\textbf{R}$)하고 이동( $\textbf{t}$)하여, $\textbf{a}’$ 가 됐음을 나타낸다.

3.1.3 Transform Matrix and Homogeneous Coordinates

회전과 이동을 여러번 했을 경우는 어떨까?

\[\mathbf{b}=\mathbf{R}_{1} \mathbf{a}+\mathbf{t}_{1}, \quad \mathbf{c}=\mathbf{R}_{2} \mathbf{b}+\mathbf{t}_{2}\]

왼쪽 식은

$\textbf{a}$ 에서 $\textbf{b}$ 로 변환(Transformation), 오른쪽 식은

$\textbf{b}$ 에서 $\textbf{c}$ 로 변환 즉, $\textbf{a}$ 에서 $\textbf{c}$ 로 변환한 경우를 말한다.

위의 식을 한번에 표현하면

\[\mathbf{c}=\mathbf{R}_{2}\left(\mathbf{R}_{1} \mathbf{a}+\mathbf{t}_{1}\right)+\mathbf{t}_{2}\]

그런데 $\textbf{a}$ 와 $\textbf{c}$ 사이에 $\textbf{b}$ 가 100개 있다고 가정했을 때 식으로 한번에 나타내기가 난감해지는데

Homogeneous coordinate를 사용하여 간단하게 만들 수 있다.

\[\left[\begin{array}{l}\mathbf{a}^{\prime} \\1\end{array}\right]=\left[\begin{array}{ll}\mathbf{R} & \mathbf{t} \\\mathbf{0}^{\mathrm{T}} & 1\end{array}\right]\left[\begin{array}{l}\mathbf{a} \\1\end{array}\right] \triangleq \mathbf{T}\left[\begin{array}{l}\mathbf{a} \\1\end{array}\right]\]

차원이 하나 추가되어 간단해졌다. 아까와 같은 가정으로 식을 한번에 나타낸다면 행렬만 앞에 100번 곱해주면 될 것이다.

또한

$\textbf{T}$ 를 Transformation Matrix라고 하며 전에 회전행렬만을 모은 집합과 똑같이 이 행렬들만 모은 집합을 생각할 수 있다.

\[\mathrm{SE}(3)=\left\{\mathbf{T}=\left[\begin{array}{cc}\mathbf{R} & \mathbf{t} \\\mathbf{0}^{\mathrm{T}} & 1\end{array}\right] \in \mathbb{R}^{4 \times 4} \mid \mathbf{R} \in \mathrm{SO}(3), \mathbf{t} \in \mathbb{R}^{3}\right\}\] \[\mathbf{T}^{-1}=\left[\begin{array}{cc}\mathbf{R}^{\mathrm{T}} & -\mathbf{R}^{\mathrm{T}} \mathbf{t} \\\mathbf{0}^{\mathrm{T}} & 1\end{array}\right]\]

$\text{SE}(3)$ 는 Special Euclidean Group이라는 의미이다.

3.3 Rotation Vector and Euler Angle

$\text{SO}(3)$ 의 Matrix는 9개의 element가 있는데 실제로 Rotation Matrix는 3 DOF라서 Matrix 표현은 좋지 못하다. 비슷하게, Transformation Matirx는 16개의 element가 있지만 실제로는 6 DOF이다.

우선 회전행렬을 다르게 표현하는 법을 알아보자.

회전이라는 것은, 어떤 축(Axis)을 기준으로 얼마만큼의 각도(Angle)로 이동했는지에 대한 관점으로 생각 할 수 있는데 이를 이용하여 회전행렬을 행렬이 아닌 vector의 형태로 표현 할 수 있다.

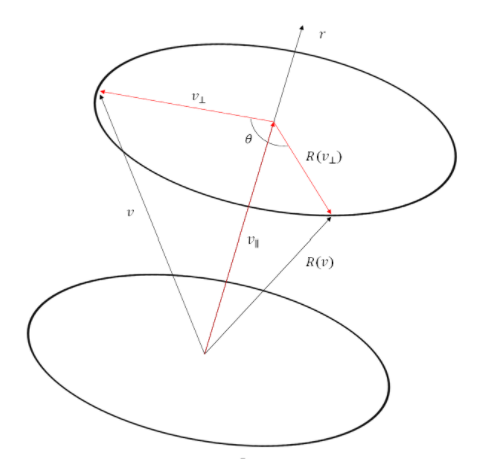
출처: https://oksujay1127.tistory.com/73

\[\mathbf{R}=\cos \theta \mathbf{I}+(1-\cos \theta) \mathbf{n n}^{\mathrm{T}}+\sin \theta \mathbf{n}^{\wedge}\]

이 식을 Rodrigues’ Formula라고 한다.

$\textbf{R}$ 을 이용해 각도를 구할 수도 있다.

\[\begin{aligned}\operatorname{tr}(\mathbf{R}) &=\cos \theta \operatorname{tr}(\mathbf{I})+(1-\cos \theta) \operatorname{tr}\left(\mathbf{n} \mathbf{n}^{\mathrm{T}}\right)+\sin \theta \operatorname{tr}\left(\mathbf{n}^{\wedge}\right) \\&=3 \cos \theta+(1-\cos \theta) \\&=1+2 \cos \theta\end{aligned}\] \[\theta=\arccos \left(\cfrac{\operatorname{tr}(\mathbf{R})-1}{2}\right)\]

회전행렬과 vector로 표현된 회전의 축($\textbf{n})$은 서로같다 따라서

\[\mathbf{R n}=\mathbf{n}\]

이 식에서 $\mathbf{n}$ 의 EigenVector가 $\textbf{R}$ 의 EigenValue 1과 대응되는 점을 알 수 있다.

3.3.2 Euler Angle

x,y,z의 축을 기준으로 회전을 나타내는 방법을 Euler Angle이라고 한다.

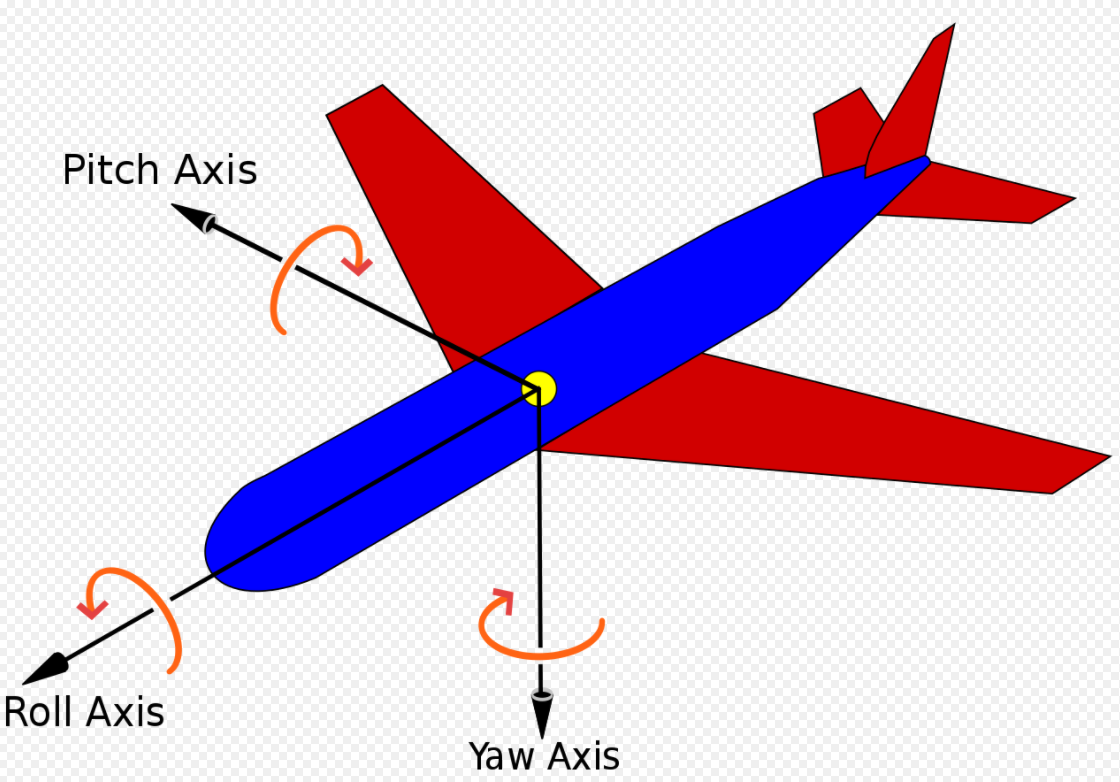
출처: https://en.wikipedia.org/wiki/Aircraft_principal_axes

그런데 잘 회전하다가 짐벌락 문제에 빠질 수 있는데 영상으로 보면 한번에 이해된다.

https://www.youtube.com/watch?v=zc8b2Jo7mno

이를 해결하기 위해 다른 수 체계를 이용한다.

다음 포스팅에 계속