Test용

Create New Map Point

1. Camera Center

1.1 Camera Parameter

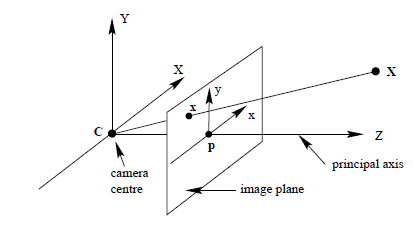
$x$ → $X$를 카메라에 projection 시켰을 때의 픽셀 좌표를 말한다.

$x$와 $X$에 대한 관계를 다음과 같이 정의할 수 있다

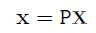
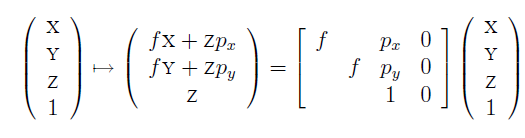
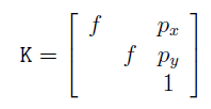
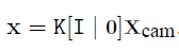
$Xcam$→ Camera coordinate 기준으로 한 $X$의 좌표

1.2 World coordinate와 Camera coordinate의 관계

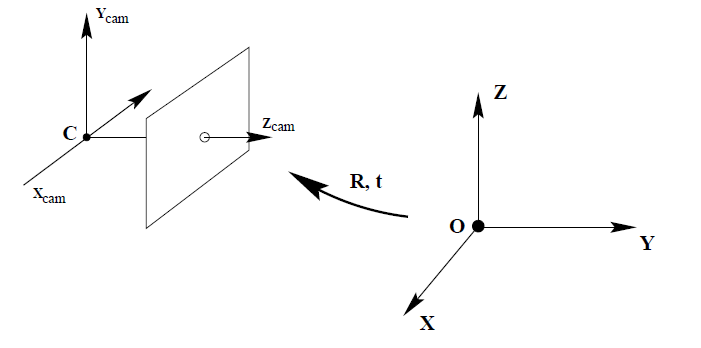
$\tilde{X}$와 $\tilde{X}cam$는 같은 위치를 각각 World Coordinate와 Camera Coordinate에서 바라본 좌표값이며 $\tilde{C}$는 Camera center이다. (위의 물결표시는 inhomogeneous임을 나타냄) 이들의 관계를 식으로 나타내면

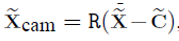
이고 이를 homogeneous로 나타내면

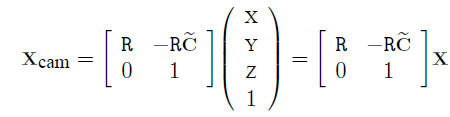
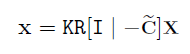
이다.

또한 $\tilde{X}cam$ 좌표는 $\tilde{X}$가 Rotation과 Translation을 했다는 관점으로 생각할 수 있다.

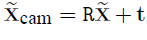
따라서, 바로 위의 식

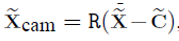
과 비교해보면

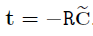
관계를 알 수 있고 $-R$을 넘겨주면 Camera Center $\tilde{C}$를 구할 수 있게된다.

2. Fundamental Matrix

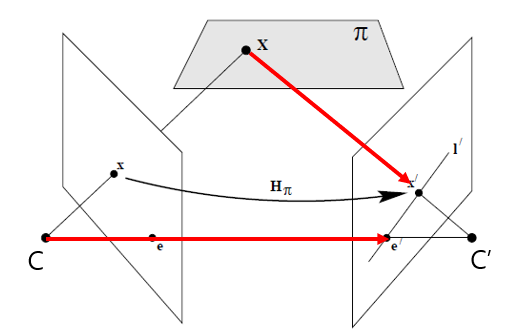
$X$를 Camera Center가 각각 $C$, $C’$인 Frame1, Frame2로 Projection된 좌표를 $x,x’$라고 하자

그러면 $C$로부터 $x$를 지나는 Ray와 $C’$로부터 $x’$를 지나는 Ray 가 $X$에서 만나며

이로 인해 epipolar plane $\pi$를 형성하게 되는데, 이는 한 평면에 $C, C’, x, x’, X$가 존재한다는 의미이다.

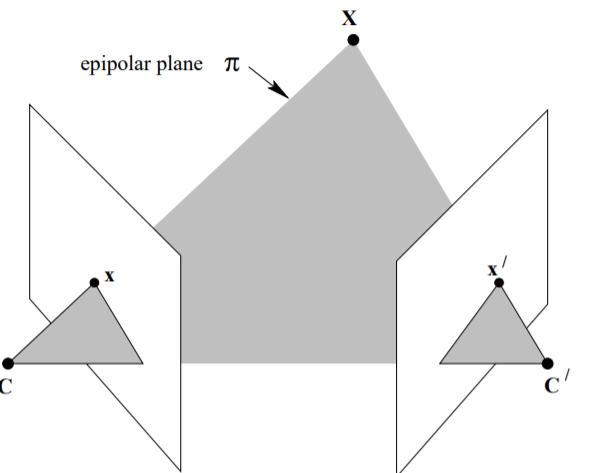
epipolar plane $\pi$와 Frame 2의 intersection은 line이 된다. 우리는 이를 epipolar line $l’$이라고 하는데

여기서 알 수 있는 것은 $x’$는 직선 $l’$위에 어딘가에 존재할 수밖에 없다는 것이다. (같은 평면에 있어야 하므로)

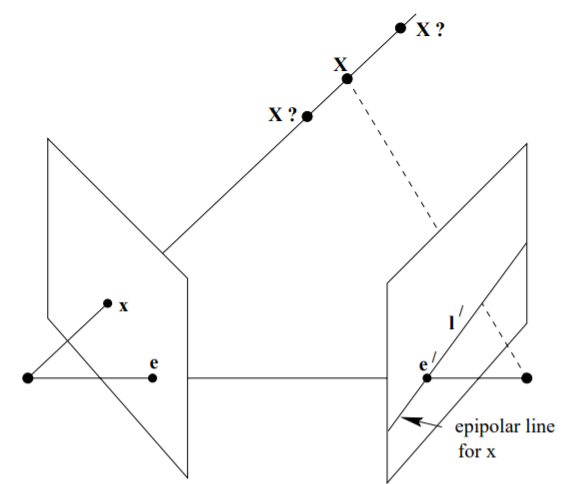
$x$에 대응되는 $l’$를 구하기 위해 $x$와 $l’$의 관계를 구해보자.

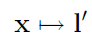
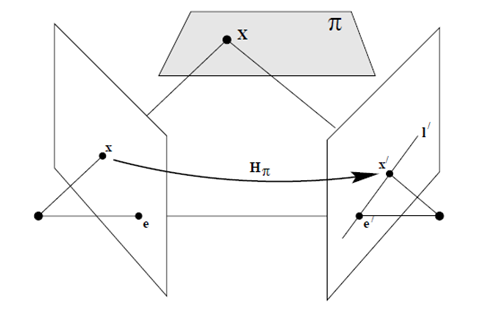
Frame1과 Frame2 위에 존재하는 $x$와 $x’$는 2D→2D mapping (Homography)의 관점으로도 볼 수 있으므로 아래와 같은 관계를 정의할 수 있다.

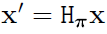
$l’$는 두 점 $e’$와 $x’$를 지나는 직선이므로 다음과 같다.

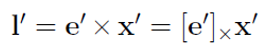
($[e’]_\times$는 skew-symmetric matrix)

따라서,

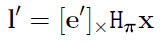
가 된다.

이제 $e’$와 $H_\pi$를 구해보자

$X$와 $x$의 관계는 1.1에서 다음과 같았다.

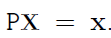
여기서 우리는 $X$부터 시작하여 $C$로 끝나는 선분의 식을 얻을 수 있다

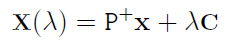
$\lambda$는 scale 값이며 $\lambda=0$일때 점 $X$를 나타내며 $\lambda=\infty$일때 점 C를 나타낸다 ($PC=0$이라 정의)

여기서 $X$는

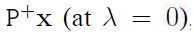
로 나타낼 수 있다.

두 점 $X$와 $C$를 Frame2로 projection 한 점이 각각 $x’,$$e’$이며 다음과 같이 정리할 수 있다.

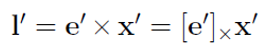
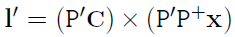
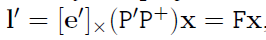
이로써 Fundamental matrix $F$를 정의할 수 있다.

ex)

만약 다음과 같은 조건이 주어진다면

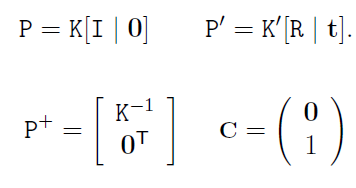
Fundamental Matrix $F$는 다음과 같이 구할 수 있다.

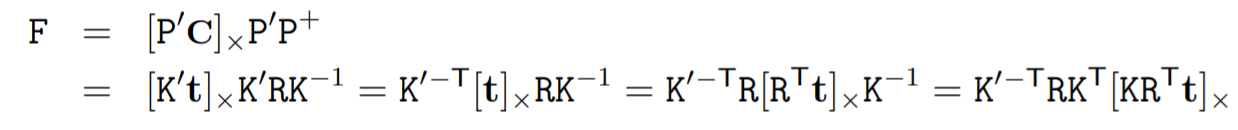
3. Linear Triangulation Method

3.1 DLT(Direct Linear Transformation)

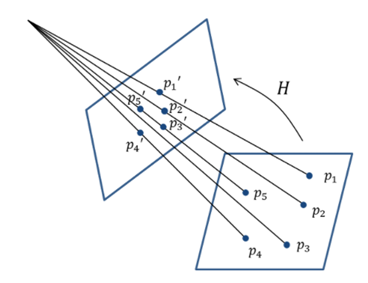
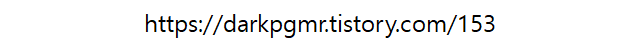
한 평면을 다른 평면에 투영(projection)시켰을 때 투영된 대응점들 사이에는 일정한 변환관계가 성립하는데 이 변환관계를 호모그래피(Homography)라 부른다.

(출처: 다크프로그래머 블로그)

이러한 변환관계는 다음과 같이 쓸 수 있다.

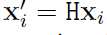
행렬 $H$의 각 행을 하나로 묶어서 행렬 $h$를 재정의 할 수 있다.

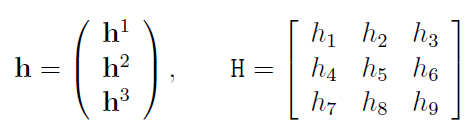
앞서말한 변한관계식에서 양변에 $x_i’$를 외적 해주고 정리하면

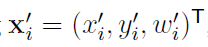
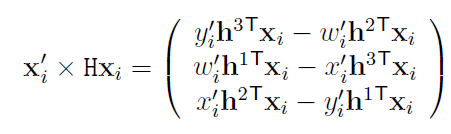
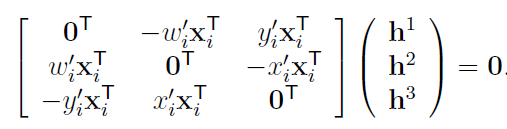
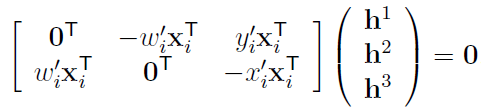
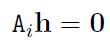
여기서 $AX=0$꼴의 식을 얻을 수 있다.

3.2 Linear Triangulation Method

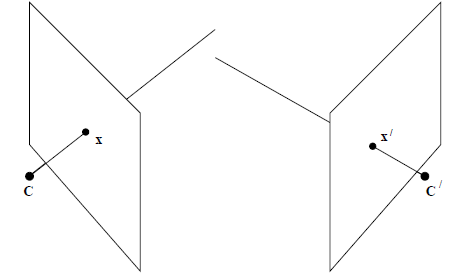
어떠한 matching을 통해 $x$와 $x’$가 같은 점을 바라보고 있다고하자

그렇다면 $x$와 $x’$가 바라보는 같은 점의 좌표를 어떻게 구할 수 있을까?

여기에 대한 해답중 하나가 Linear Triangulation Method 이다.

두 점 $x$와 $x’$는 다음과 같은 관계를 갖는다.

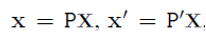
여기서 특정한 행렬 A를 얻을 수 있다.

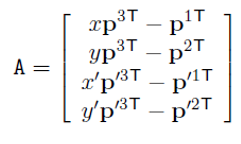
이 특정한 행렬을 얻는 방법은 3.1에서 말한 DLT(Direct Linear Transformation)로부터 유도될 수 있다.

현재 우리가 구해야 하는 좌표는 X이므로 식은 다음과 같다.

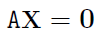
3.3 Least-squares solution

앞서 본 식에 완벽하게 맞는 X를 찾을 수 있으면 좋겠으나, noise같은 문제 때문에 정확한 값을 구할 수는 없고 $AX=0$ 를 만족시키는 값과 가장 가까운 X를 찾아야 한다.

이는 Least-square minimization 문제이며 최적화를 위해 여기서는 SVD를 이용한다

(SVD에 대한 설명 https://angeloyeo.github.io/2019/08/01/SVD.html )

$X$가 0이면 의미가 없으므로 $|X|=1$ 이라는 제약 조건을 추가해주면 다음과 같은 최적화 문제를 만들 수 있다.

$Minimize$ $\newcommand{\norm}[1]{| #1 |}$$|AX-b|=|AX|$

$Subject\ |X|=1$

$A=UDV^T$ 라고 하면(SVD) 주어진 문제는 $|UDV^TX|$를 최소화 해주는 문제로 바뀐다

Norm-preserving 성질 때문에 다음과 같은 두 식을 얻을 수 있다.

$|UDV^TX|=|DV^TX|$ $|X|=|V^TX|$

여기서 $V^TX$를 $y$로 놓는다면 다음과 같은 최적화 문제를 만들 수 있다.

$Minimize\ |Dy|$

$Subject\ |y|=1$

이 문제에 대한 솔루션은 $y=(0,0,0,…,1)^T$ 이다.

$y=V^TX$에서 $X=Vy$ 이므로 최종적으로 $X$는 $V$의 마지막 열(Column)과 같다는 말이다.

요약하면 다음과 같다

이로써 $X$에 대한 값을 구할 수 있게 된다.

3.4 Reprojection Error

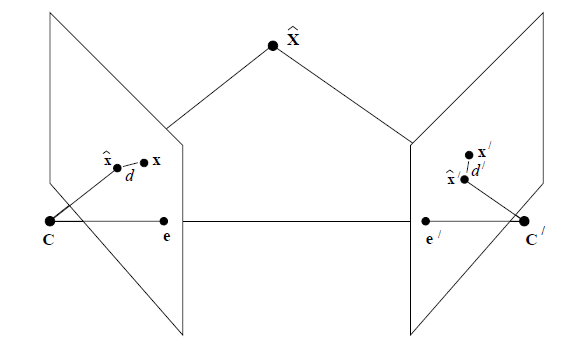
바로 이전에 구한 점 $X$ (그림에선 $\hat{X})$에 대해서 Camera Center가 $C, C’$인 Frame 1과 Frame 2에 각각 다시 projection 시키면 $\hat{x}$, $\hat{x}’$을 얻을 수 있게 되는데 앞서 매칭된 점 $x, x’$와 차이가 있다.

$x$와 $\hat{x}$의 Euclidean distance와 $x’$와 $\hat{x}’$의 Euclidean distance의 합을 cost function으로 새로 정의해준다.

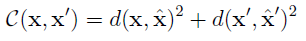
ORB SLAM 3 코드 내에서는 이 cost function이 일정 값 이상이면 continue 문을 수행하는 하는 것으로 추정된다.